稀疏矩阵的概念
一个m×n的矩阵是一个由m行n列元素排列成的矩形阵列。矩阵里的元素可以是数字、符号及其他的类型的元素。
一般来说,在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非0元素数目占大多数时,则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度,下面的矩阵就是一个典型的稀疏矩阵。
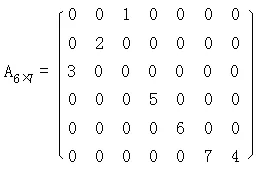
我们日常使用的电子表格也是一个典型的稀疏矩阵场景,电子表格(SpreadJS, Excel,Google Sheet等等),整体看起来像一个table表格。
其中列名称依次为A, B, C … …, 行名称依次为1, 2, 3 … …
举例一个比较极端的场景,在A1和ZZ2000单元格分别赋值,这样我们就需要一个2000行,26*26+26=702列的矩阵来表示它,这个矩阵是一个明显的稀疏矩阵。
稀疏矩阵的存储方式及优化
直接存储为二维矩阵
直接使用二维矩阵会简单直接地存储整个电子表格,这样你不必每次都创建或删除一段内存。
但这是一种非常暴力的存储值的方法,这种方式下会消耗大量内容来存储毫无内容的单元格。
简单来看一下它的复杂度:
- 占用空间:O(N2)
- 插入数据:需要破坏矩阵.
- 删除数据:需要破坏矩阵.
- 搜索数据:O(N2)
- 访问数据:O(1)
N是假设行和列具有相同长度并形成正方形矩阵的行/列数。
通过键值对(Map, Dictionary)优化
在这种方法中,只有在单元格有值时,我们才将单元格的值和位置存储在一起,使用HashMap或者Dictionary这些数据结构可以很容易的做到。
下图我们可以看到,键值对中分别存储了单元格位置和单元格值。

来看一下它的复杂度:
- 空间:O(N)
- 插入:O(1)
- 删除:O(1)
- 搜索:O(N)
- 访问:O(1)
N为所记录的条目数。
通过稀疏矩阵存储方式优化
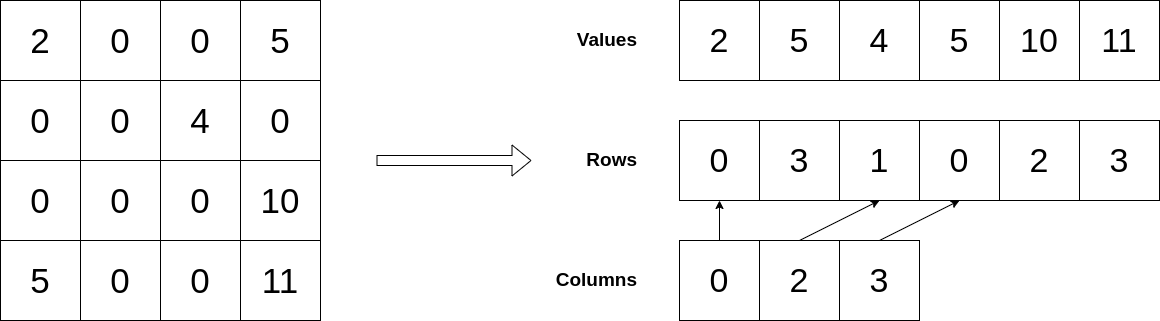
在稀疏矩阵中,我们可以使用三个不同的数组来存储行索引、列偏移、和其中的值,而不是直接在二维矩阵中存储值。以这种方式按列压缩稀疏矩阵存储的三个数组:
值 =>单元格中的值。
行索引=>单元格的行索引。
列偏移=>这里每个索引都代表列,并且该数组将行开始的索引值存储在 Row 数组中。
左图中的稀疏矩阵被存储为右图的三个数组:
稀疏矩阵具体的插入、删除、搜索、访问的代码,大家可以自己来搜索,这方面的资料网上有很多,这里不一一列举。
和上面一样,来看看这种方式的复杂度:
- 空间:O(N)
- 插入:O(N)
- 删除:O(N)
- 搜索:O(N)
- 访问:O(1)
相较于传统的数组存储或是键值对存储,稀疏矩阵存储构建了基于行索引为 Key 的数据字典,在松散布局的表格数据中,稀疏矩阵只会对非空数据进行存储,而不需要对空数据开辟额外的内存空间。使用这种特殊的存储策略,使得数据片段化变得容易,可以随时框取整个数据层中的一片数据,进行序列化或反序列化。如果我们在项目开发中需要存储类似结构的数据,稀疏矩阵这种存储方式,无论从时间还是空间上都能大大的提成性能。
在葡萄城的 SpreadJS 和 GcExcel 表格组件中,也巧妙的使用了稀疏矩阵这一特性,可以随时替换或恢复整个存储结构中的任何一个级别的节点,以改变引用的方式更高效地解决表格数据回滚和恢复问题,而这一点也为葡萄城表格组件支持多人在线协同打下了一个良好的基础。
由于底层采用了稀疏矩阵来优化存储,SpreadJS在前端页面中,实现了100W级别数据秒级响应的能力:
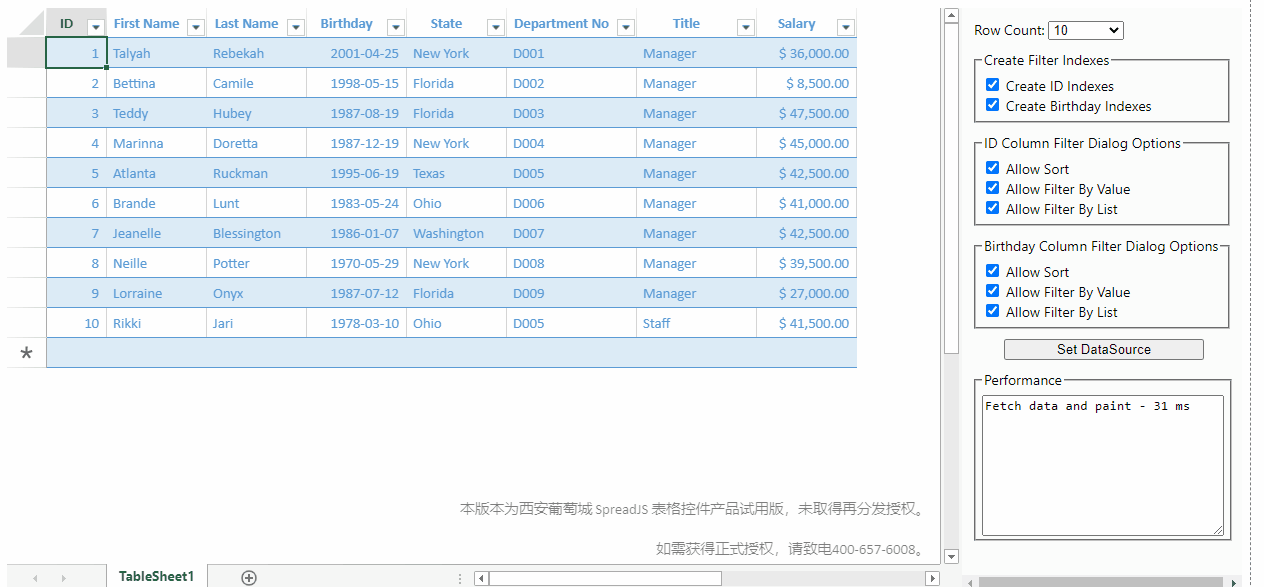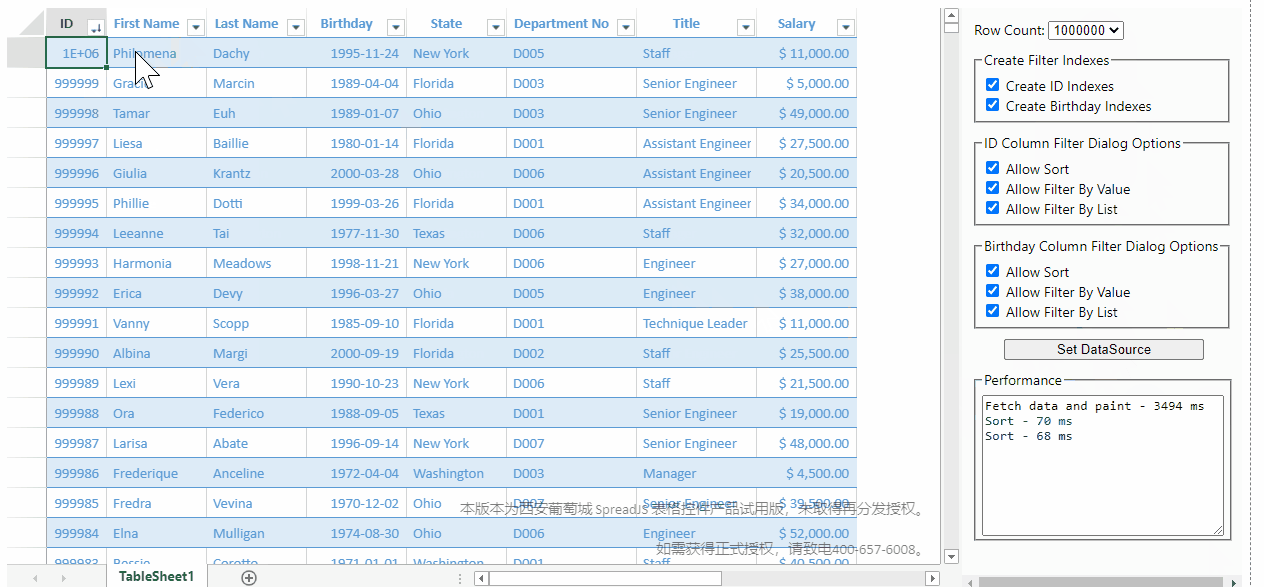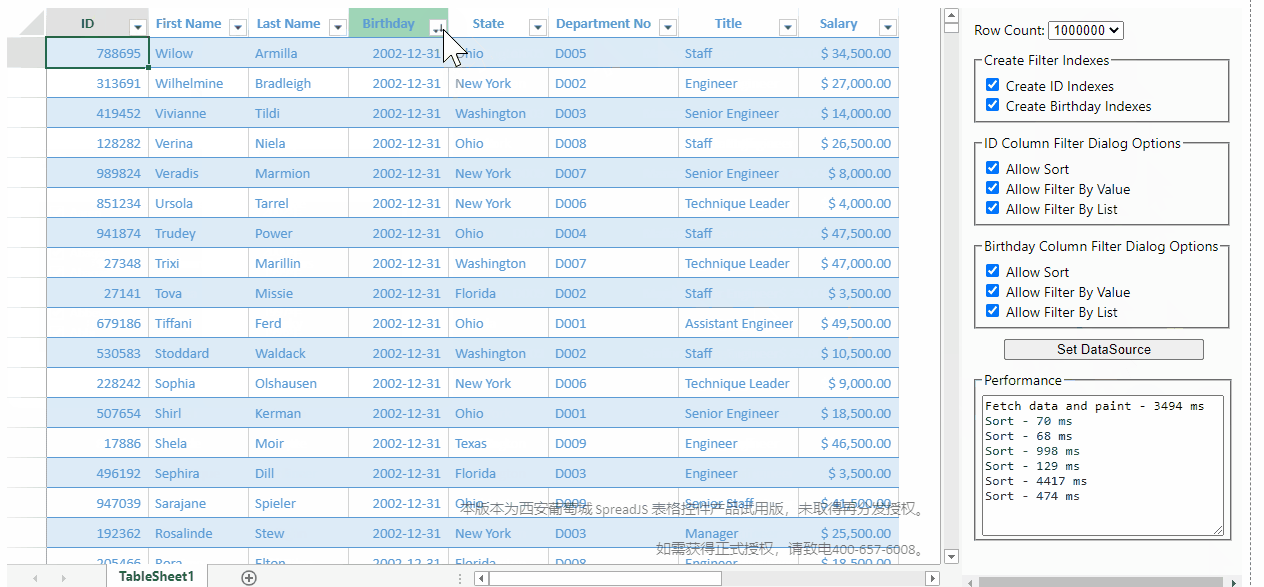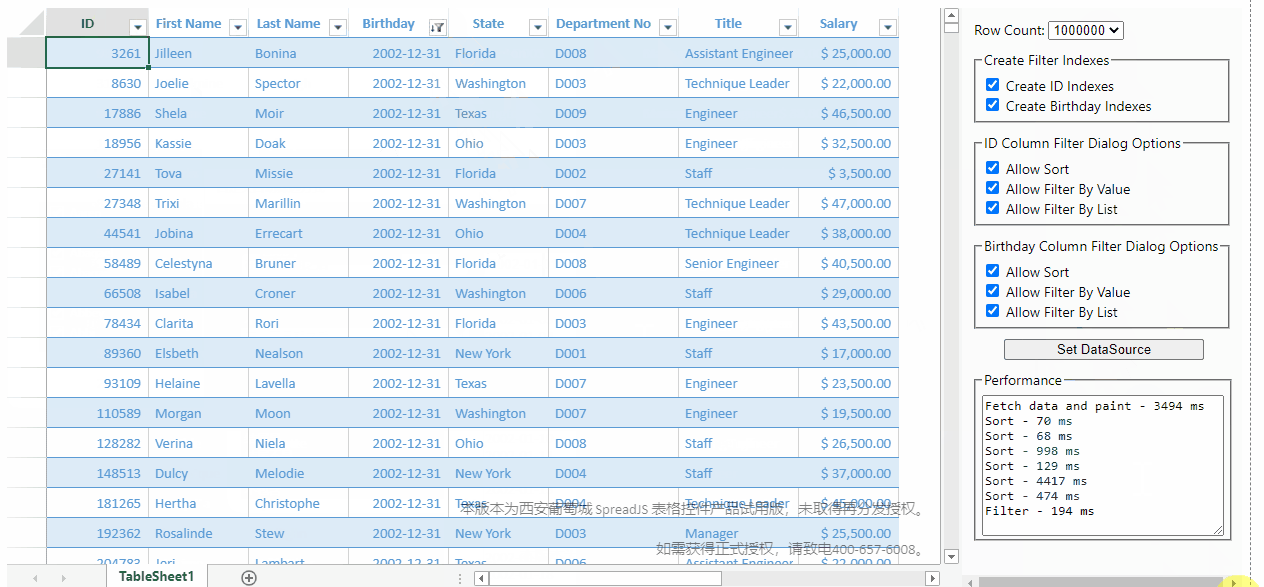
点击此处可以在线体验:性能演示
同时,结合SpreadJS中使用的Canvas 绘制模型,双缓存画布渲染等专利技术,让SpreadJS的前端性能相比于同类产品遥遥领先。
更多纯前端表格在线demo示例:https://demo.grapecity.com.cn/spreadjs/gc-sjs-samples/index.html
纯前端表格应用场景:https://www.grapecity.com.cn/developer/spreadjs\#scenarios
移动端示例(可扫码体验):http://demo.grapecity.com.cn/spreadjs/mobilesample/